http://www.matjazev.net/blog/2012/10/16/edinstvene-vrednosti-v-excelu-ii/ kako prešteti edinstvene vrednosti znotraj nekega Excelovega območja in prišli do spoznanja, da omenjena formula deluje samo nad številskimi podatki.
V kolikor pa se med vrednostmi nahajajo tudi nizi znakov, datumi ali kaj tretjega pa opisana metoda odpove.
Poiskati je torej potrebno način, ki bo preštel različne vrednosti neglede na njihovo vsebino. Iščemo torej bolj splošno formulo, ki jo bomo lahko uporabili vedno.
Seveda se sprašujete zakaj nisem te formule zapisal že takoj na začetku saj bo očitno delovala nad vsemi tipi podatkov in je zatorej boljša kot tista, ki sem vam jo predstavil zadnji. Odgovor je seveda v zahtevnosti.
Današnja formula je celo krajša in lepša od FREQUENCY, a je težje razumljiva oz. vem priporočam, da se poglobite v razumevanje zakaj deluje oz. zakaj vrača pravilen rezultat.
Uporabljene formule
Za končni rezultat bomo potrebovali dve vgrajeni Excelovi funkciji SUMPRODUCT in COUNTIF. Funkcijo COUNTIF sem v blogu že opisoval, SUMPRODUCT pa še nisem omenjal.
COUNTIF funkcije preprosto prešteje število celic, ki ustrezajo nekemu pogoju, funkcija SUMPRODUCT pa je bolj podobna mrežnim funkcijam in medsebojno sešteva medsebojne rezultate.
IDEJA REŠITVE
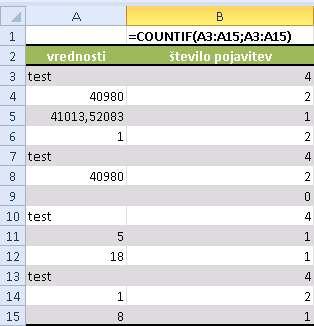
Za vsako celico bomo ugotovili kolikokrat se pojavi na celotnem območju (temu bo služila funkcija COUNTIF).
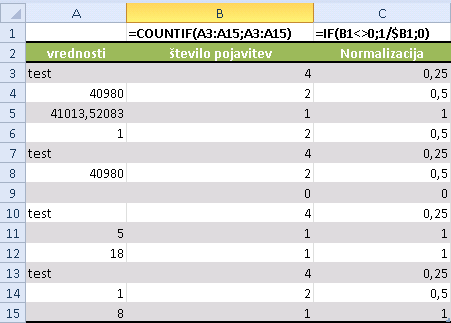
Sedaj je potrebno te podatke normalizirati, kar pomeni, da če se neka vrednost pojavi N krat, jo bomo mi upoštevali samo 1/N krat… Z drugimi besedami – vse rezultate je potrebno potencirati na -1 oz. 1 deliti z njimi:
Kot vidite lahko normalizirane vrednosti preprosto seštejemo (zato smo jih normalizirali!) dobimo iskani rezultat – število edinstvenih vrednosti ne nekem območju.
In če sedaj opisano idejo zapišemo z eno formulo dobimo sledeč rezultat:
=SUMPRODUCT((A3:A15<>"")/COUNTIF(A3:A15;A3:A15&""))
In to je splošna formula štetja edinstvenih vrednosti v Excelu!